CHEMISTRY:
Pulling Strings

Walter Fontana*

Computing devices, like the information they process, are embodied in a material substrate constrained by the laws of physics (1). The design of modern computing devices has nevertheless succeeded to a remarkable extent in separating hardware from software and questions specific to physics from questions specific to computation. In such a setting, abstract formalisms of the kind envisioned by Turing (2) can justifiably ignore the nature of materials and issues such as energy dissipation and material stability.

However, this separation between hardware and software--and hence physics and computation--breaks down when device features approach atomic scales or when the devices that process information are of the same class as the information itself. How, then, can we realize computation in the world of molecules and their chemical reactions? On page 1585 of this issue, Seelig et al. (3) provide an answer to this question.

One way to formally express computation is in terms of rules that rewrite words. Molecules, like words, are combinatorial structures, and chemical reactions can provide the required rules, if we can program chemistry. To exert the necessary control over chemistry, we must be able to specify which components in a mixture of molecules interact when, and where. This control can be achieved by designing appropriate single-stranded DNA (or RNA) sequences that bind to each other like Velcro's hook and loop fasteners, but in an addressable manner. Based on this idea, Seelig et al. exploit a simple principle--strand displacement--to implement not just logic gates, but also a toolkit of devices for building molecular circuits of a digital kind.

In the past decade, DNA (or RNA) sequences have been used to find solutions to combinatorial problems by self-assembly (4), to encode complete decision trees for simple games like tic-tac-toe (5), and to build programmable sensors of cellular states (6). DNA has also been used to build nanostructures and nanomechanical devices (7, 8), as well as two-dimensional grids that can function as frames of reference for placing such devices at specific locations (9). For example, Seeman and co-workers (10) have developed a rotary device that consists of two DNA strands woven into two pairs of helices, with a flexible hinge region in between. This device can act as a programmable, molecular-scale robot arm. On page 1583 of this issue, Ding and Seeman (11) report the deliberate, function-preserving placement of such a device in a two-dimensional array of DNA tiles.

There are two reasons for the versatility of DNA as a structural, mechanical, and computational substrate. First, the Watson-Crick base-pairing rules provide a natural foundation for programming the interaction specificity of DNA sequences. Second, base pairing provides the free energy needed to deliberately change structures and move computation forward. A DNA strand will let go of its binding partner if a third strand offers base pairs that are energetically more favorable. A DNA sequence thus serves both as a specific instruction and as the fuel needed for its own execution.

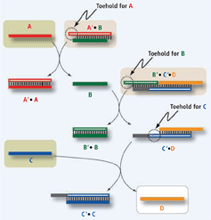
To illustrate the case of Seelig et al., consider two sequences A' and B that form a complex A'B by virtue of complementary segments. In the presence of a strand A that offers more favorable base pairs to A' than B, a displacement reaction A + A'B AA' + B will occur (see the figure). The DNA complex A'B therefore stands for the statement "if A then B', because it yields B when it encounters A. In this scheme, the gate "B AND C" translates into a statement like "if (B and C) then D", which is a DNA complex designed to release strand D as a result of two sequential displacement reactions that require the presence of B and C (see the figure).

Gate composition.
The translator gate A'B (gray box in top row) exchanges strand A for B. B then triggers the "B AND C" gate (B'C'D, gray box in second row). Together, the two gates form an "A AND C" gate that emits a Dstrand in the presence of inputs A and C (light green boxes). Open and filled bars represent complementary sequence segments. If D were A (or give rise to A, as accomplished by a translator D'A), the end product could reenter the cascade at the top, creating a feedback loop.

In such a system, logic gates are molecular (DNA) complexes that execute their logic through reactions. Gates constructed in this way can be concatenated, because the output string released by one gate can react with another gate in the mixture, much like in biological signaling cascades. For example, an "A AND C" gate can be implemented by using a "B AND C" gate in conjunction with an "if A then B" construct that exchanges A for B (see the figure). This is analogous to address forwarding in a Web browser.
A test tube typically contains many copies of a given gate complex that undergo displacement reactions in accordance with the binding preferences programmed into their DNA sequences. Because these reactions yield a noisy output-strand concentration, digitization of the output yield as "high" (true) or "low" (false) is required to interpret a DNA gate as a logic operation.

Seelig et al. provide a toolkit of DNA-based reactions for such digital signal processing. The tools include thresholds to remove leaks and amplifiers to restore signal strength. For example, an amplifier permits one input strand to cause the release of more than one output strand copy. This can be achieved by a feedback construct involving two gates that mutually trigger each other ("if A then B + if B then A") as soon as input strand A appears in the mixture. Alternatively, the input strand has been used as a catalyst for refolding a metastable DNA complex in a process that also releases an output strand (12). In this way, the same input strand can help to refold several complexes, leading to output amplification.

It can be difficult to design sequences that make up large circuits. Complementary regions in a DNA sequence can cause a strand to fold back upon itself, potentially blocking further computation. Accidental complementarities across sequences can lead to interference between computations, in analogy to cross-talk in biological signaling systems. Seelig et al. use a computational optimization procedure to design sequences that minimize the likelihood of such complications. They validate their architecture and design tools with a dazzling circuit of 11 gates and six inputs.

What might this prototype technology be good for? The authors envision analytical applications in systems biology, such as the in situ detection, quantification, or amplification of microRNAs and transcription patterns. But this scalable molecular programming language may also provide a means for choreographing the assembly and operation of future nanometer-scale devices.

Unlike electronic circuit elements, DNA gates and their inputs are used up as the computation unfolds through chemical reactions; hardware and software are one and the same. Yet, what appear to be limitations may turn out to be intriguing opportunities. As gates are transformed by the very computations they control, can new gates assemble as by-products? Could one devise a computational gate "metabolism" that maintains an ensemble of gates through a catalytic cycle?

Milner has devised a calculus (13) that views every component of a distributed computational system as an interactive process, whose channels are consumed upon communication. Seelig et al. may unknowingly have come close to implementing design aspects of that calculus in chemistry. Theoretical computer scientists may find inspiration in a chemical model of an influential abstraction. In return, modifications of this calculus may become useful in the design and analysis of DNA gate systems.

Over the past half-century, the idea has taken hold that physical processes, particularly in biological systems, can be understood as computation. A back-and-forth between transparent experimental models of molecular computation and the development of formal tools for reasoning about concurrent behavior might lead to a better appreciation of what it means for cells to "compute," "organize," or "process information" and, perhaps, evolve.

References